Pache.co Information Technologies

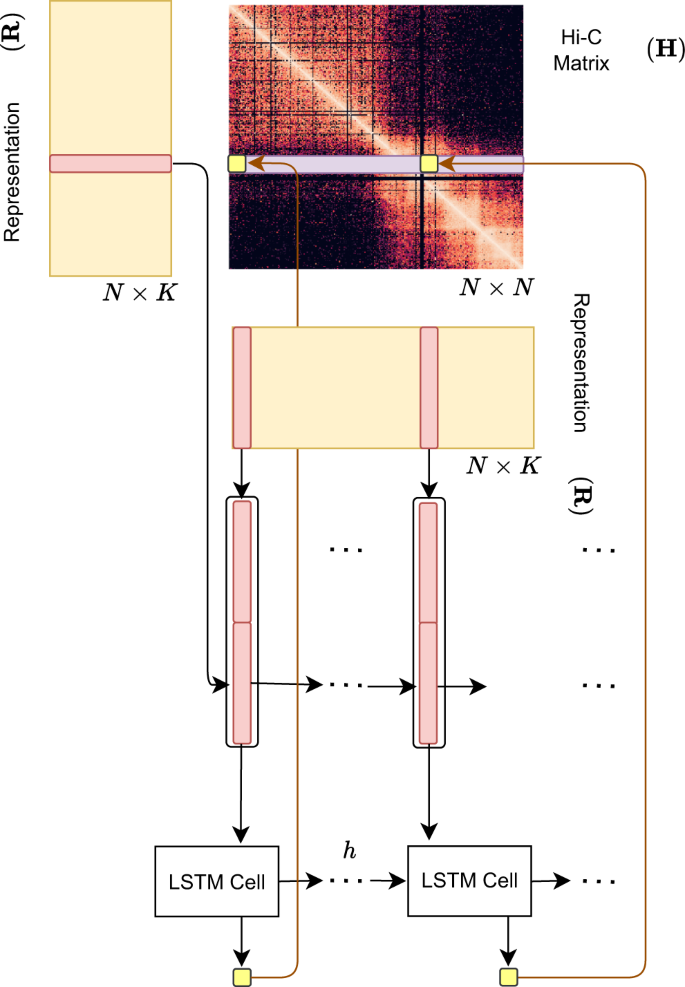
Hi-C-LSTM representations capture the information needed to create the Hi-C matrix

Hi-C-LSTM assigns a representation to each genomic position in the Hi-C contact map, such that a LSTM⁴¹ that takes these representations as input can predict the observed contact map (Fig. 2). The representation and the LSTM are jointly trained to optimize the reconstruction of the Hi-C map. This process gives us position-specific representations genome-wide (see the “Methods” section for more details).

A trained Hi-C-LSTM model consists of a K-length representation R_i for each genomic position i and LSTM connection weights (see the “Methods” section). To predict the contact vector of a position i with all other positions, the LSTM iterates across the positions j ∈ {1…N}. For each (i, j) pair, the LSTM takes as input the concatenated representation vector (R_i R_j) and outputs the predicted Hi-C contact probability H_i,j. The LSTM hidden state h is carried over from (i, j) to (i, j + 1). This process is repeated for all N rows of the contact map by reinitializing the LSTM states. The LSTM and the representation matrix are jointly trained to minimize the reconstruction error.

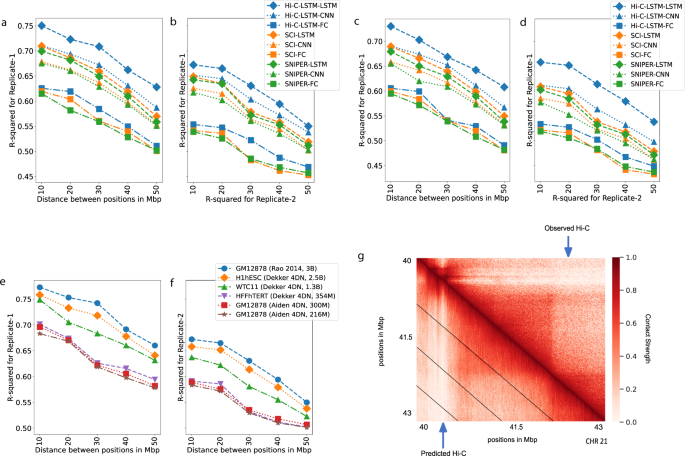
We find that Hi-C-LSTM achieves higher accuracy when constructing the Hi-C matrix compared to existing methods (Fig. 3a, c). The inferred Hi-C map matches the observed Hi-C map (Fig. 3g) closely, and differs from it by about 0.25 R-squared points on average. We adapt SNIPER to our task by replacing the feed-forward decoder that converts low-resolution Hi-C to high-resolution Hi-C with a decoder that reproduces the observed input Hi-C. We call this SNIPER-FC. Hi-C-LSTM outperforms SNIPER (SNIPER-FC) convincingly, by 10% higher R-squared on average (Fig. 3a). Hi-C-LSTM also outperforms SCI (SCI-LSTM) by 12% higher R-squared on average (Fig. 3a).

a, b The Hi-C R-squared computed using the combinations of representations from different methods and selected decoders for replicate 1 and 2 (GM12878). The horizontal axis represents the distance between positions in Mbp. The vertical axis shows the reconstruction accuracy for the predicted Hi-C data, measured by average R-squared. The R-squared was computed on a test set of chromosomes using selected decoders with the representations trained all chromosomes as input. The legend shows the different combinations of methods and decoders, read as [representation]-[decoder]. c, d Same as (a, b), but for H1-hESC. e, f Hi-C R-squared computed for different cell types. g A selected portion of the observed Hi-C map (upper-triangle) and the predicted Hi-C map (lower-triangle) in GM12878. The portion is selected from chromosome 21, between 40 and 43 Mbp. Diagonal black lines denote Hi-C-LSTM’s frame boundaries (see the “Methods” section).

Two hypotheses could explain Hi-C-LSTM’s improved reconstructions: (1) that Hi-C-LSTM’s representation captures more information, or (2) that an LSTM is a more powerful decoder. We found that both are true. To distinguish these hypotheses, we split each model, respectively, into two components—its representation and decoder—and evaluated each possible pair of components. We train the representations (Hi-C-LSTM, SCI, SNIPER) on all chromosomes and couple them with selected decoders (LSTM, CNN, FC). Using the representations as input, we re-train these decoders with a small subset of the chromosomes and test on the rest. (see the “Methods” section for more details). We compute the average R-squared value for creating the Hi-C contact matrix using each combination of selected representations and decoders

We found that the choice of decoder has the largest influence on reconstruction performance. Using a LSTM decoder performs best, even when using representations derived from SNIPER or SCI (improvement of 0.14 and 0.12 R-squared points on average over fully connected decoders, respectively, Fig. 3a). Furthermore, we found that Hi-C-LSTM’s representations are most informative, even when using decoder architectures derived from SNIPER or SCI (Fig. 3a).

Though the Hi-C-LSTM representations capture important information from a particular sample, we wanted to verify whether they capture real biological processes or irreplicable experimental noise. To check the effectiveness of Hi-C-LSTM representations in creating the Hi-C contact map of a biological replicate, we train the representations on one replicate (replicate 1), repeat the decoder training process on replicate 2 (see the “Methods” section for more details), and compute the average R-squared value for creating the Hi-C contact map of replicate 2 (Fig. 3b, d). The average R-squared reduces slightly for inference of replicate 2 due to experimental variability; however, the performance trend of the representation–decoder combinations is largely preserved (Fig. 3b, d). These results show that Hi-C-LSTM’s improved performance is not merely driven by memorizing irreplicable noise.

We discovered a relationship between sequencing depth and model performance after training and evaluating Hi-C-LSTM on Hi-C datasets from GM12878 with a combined filtered reads of 300 million and 216 million (compared to Hi-C data from Rao et al. which had 3 billion combined filtered reads). We saw that Hi-C-LSTM R² worsened with reduced read depth, however, the reconstruction performance trend over distance was preserved (Fig. 3e, f).

We also trained and evaluated Hi-C-LSTM on data from 3 other tier 1 cell types from the 4DN Data Portal apart from GM12878, namely, H1-hESC (embryonic stem cell) (Fig. 3c, d), HFF-hTERT (foreskin fibroblast immortalized cell) (Supplementary: Fig. 1a, b), and WTC11 (induced pluripotent stem cell derived from skin leg fibroblast) (Supplementary: Fig. 1c, d). We found that difference in performance across these cell types can be explained by their differing read depths. These data sets have varying read depths, ranging from 150 million (HFFhTERT) to 900 million (H1hESC) filtered reads. We saw that the R² fell by 0.03 points on average when reads reduced from 3 billion to 1 billion (Fig. 3e). The performance further reduced by 0.4 on average when the reads reduced to 150 million. This amounted to a total R² decrease of 0.7 points on average with very low sequencing depth (Fig. 3e). We additionally found that the reconstruction performance trend between models is preserved across cell types (Supplementary: Fig. 1).

Hi-C-LSTM representations locate functional activity, genomic elements, and regions that drive 3D conformation

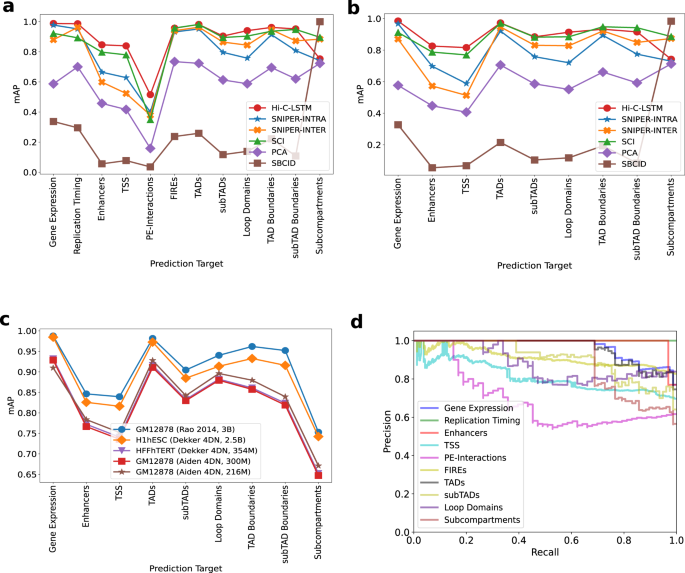
Considering that a good representation of Hi-C should contain information about the regulatory state of genomic loci, we evaluated our model by checking whether these genomic phenomena and regions are predictable from only the representation. Specifically, we test whether the position specific representations learned via the Hi-C contact-generation process are useful for genomic tasks that the model was not trained on, such as classifying genomic phenomena like gene expression⁴² and replication timing^43,44,45,46, locating nuclear elements like enhancers, transcription start sites (TSSs)⁴⁷ and nuclear regions that are associated with 3D conformation like promoter–enhancer interactions (PEIs)^48,49,50, frequently interacting regions (FIREs)^51,52, topologically associating domains (TADs), subTADs, and their boundaries¹⁸, loop domains and subcompartments¹⁸. We compared two classifiers, a boosted decision tree (XGBoost) model⁵³ to predict binary genomic features of GM12878 from representations, for each task separately, and a multi-class multi-label model with a simple linear layer and sigmoid, to predict all tasks from the representations simultaneously (see the “Methods” section for more details regarding comparison methods, baselines and classifiers).

We use mean average precision (mAP) (see the “Methods” section) to quantify classification performance (for additional classification metrics like area under the receiver operating characteristic curve (AuROC), F-score, and Accuracy, refer to the Supplementary, see the “Methods” section for definitions). We find that the models built using the intra-chromosomal representations achieve higher classification performance overall relative to ones trained on inter-chromosomal representations when predicting gene expression, enhancers and TSSs (Fig. 4a, b). This trend is likely due to the relatively close range of the elements involved in prediction. We verify this observation by running Hi-C-LSTM at different resolutions (see the section “Resolution”). In contrast, SNIPER is slightly better at predicting replication timing when compared to the rest of the intra-chromosomal models except Hi-C LSTM (SNIPER-INTER, Fig. 4a, b). While all methods achieve low absolute scores at predicting promoter–enhancer interactions, Hi-C-LSTM performs best (0.5 units on average, 0.1 unit higher on average than SCI) (Fig. 4a, b, d).

a Prediction accuracy for gene expression, replication timing, enhancers, transcription start sites (TSSs), promoter–enhancer interactions (PEIs), frequently interacting regions (FIREs), loop and non-loop domains, and subcompartments in GM12878. The y-axis shows the mean average precision (mAP), the x-ticks refer to the prediction targets, and the legend shows the different methods compared with. b Same as (a), but for targets in H1-hESC. c mAP using Hi-C-LSTM for targets compared across cell types. d The Precision-Recall curves of Hi-C-LSTM for the various prediction targets in GM12878. The y-axis shows the Precision, the x-axis shows the Recall, and the legend shows the prediction targets.

Both methods perform comparably in predicting the other interacting genomic regions like FIREs, TADs, subTADs, loops domains, and subcompartments (Fig. 4a, b). SNIPER-INTRA as well as SNIPER-INTER do not perform as well as Hi-C-LSTM and SCI on these tasks. One caveat of the model is that it loses CTCF interaction dots at loop boundaries because of its sequential prediction streaks (Supplementary Fig. 2).

The only task on which other methods outperform Hi-C-LSTM is at predicting subcompartments. Subcompartments were originally defined based on inter-chromosomal interactions, so representations based on such interactions outperform those based on intra-chromosomal interactions such as Hi-C-LSTM (see Supplementary: Fig. 3 for confusion matrix). Also subcompartment-ID (SBCID) methods achieves perfect mAP by virtue of its design (Fig. 4a, b). Among the rest of the methods, we find that methods which were designed to predict subcompartments such as SCI and SNIPER-INTER, perform better than the others (Fig. 4a, b). Hi-C-LSTM does perform marginally better than SNIPER-INTRA. Overall, although Hi-C LSTM performs better than other models on most of the tasks, the performance of SCI and SNIPER are comparable to Hi-C-LSTM and all three models perform significantly better than the baselines on average (Fig. 4a, b).

Similar to reconstruction, when comparing classification performance across cell types, we saw that Hi-C-LSTM accuracy worsened with reduced read depth. However, the classification performance trend over tasks was preserved (Fig. 4c). We include results for all available data sets for each cell type. We omitted WTC11 from this analysis because most data sets are not available (see the “Methods” section for details regarding element specific data in cell types). We observed that the accuracy reduced by 0.6 units on average when the reads reduced to 150 million (Fig. 4c). Next, we compared the classification performance of Hi-C-LSTM with other methods (SCI, SNIPER) and baselines (PCA, SUBCOMPARTMENT-ID) in these cell types (Supplementary Figs. 4–6). Similar to R², we saw that the prediction score trend of methods is preserved across all these cell types.

Understanding what kind of interactions the model is more likely to capture is vital. TADs are identified with a higher accuracy in all cell types compared to other larger chromatin structures like subcompartments (Fig. 4a, b; Supplementary: Fig. 4–6). On the other hand, Promoter-Enhancer interactions are hard to classify in all cell types (Supplementary: Fig. 4,5,6). This means that Hi-C-LSTM representations achieve higher accuracy for medium-scale structures such as TADs than for small-scale structures like promoter–enhancer interactions. This could be due to many factors including data resolution, model architecture, and conservation across cell types.

Hi-C-LSTM recapitulates structures at different Hi-C resolutions

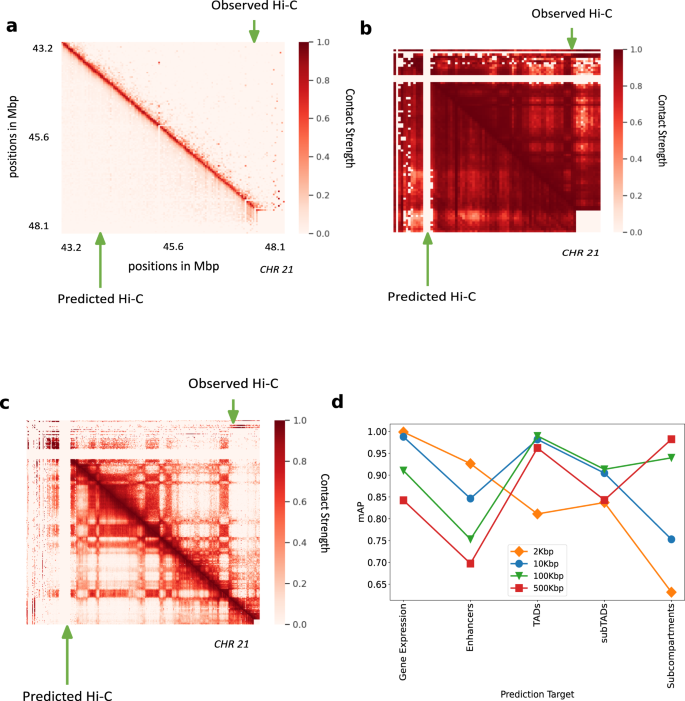
To check if Hi-C-LSTM works at different resolutions of Hi-C data, in addition to our model trained at 10 kbp, we trained Hi-C-LSTM at three other resolutions of 2, 100, and 500 kbp. As expected, models at different scales detect different elements, classify differently, and attribute importance to different sites depending on the resolution. The models achieved these by forming representations that allowed them to construct the Hi-C map at the given resolution. We investigate how these representations differ from the ones learned at 10 kbp.

To train the model at 2 kbp, we used only a subset of chromosomes due to memory and compute constraints but trained on the whole genome at other resolutions. A selected portion in chromosome 21 (Fig. 5a) shows that the predicted Hi-C values capture the fine structure of Hi-C even at 2 kbp resolution. The sparsity of available data at 2 kbp is a major constraint in enhancing the performance of the model at this resolution. Hi-C-LSTM captures the Hi-C macro-structures accurately at 500 kbp (Fig. 5b) and 100 kbp (Fig. 5c). This is because operating at this resolution with our sequence length allows it to span entire smaller chromosomes.

a Hi-C-LSTM predictions at 2 kbp resolution. A selected portion of the observed Hi-C map (upper-triangle) and the predicted Hi-C map (lower-triangle) in GM12878. The portion is selected from chromosome 21, between 43.2 and 48.1 Mbp. b Hi-C-LSTM predictions at 500Kbp resolution. The observed Hi-C map (upper-triangle) and the predicted Hi-C map (lower-triangle) in GM12878 for chromosome 21. c Hi-C-LSTM predictions at 100 kbp resolution. The observed Hi-C map (upper-triangle) and the predicted Hi-C map (lower-triangle) in GM12878 for chromosome 21. d The classification performance (as measured in mAP) with gene expression, enhancers, TADs, subTADs, and subcompartments of models trained at different resolutions.

We found that representations at different resolutions predict chromatin structures of different scales. The classification performance (as measured in mAP) with gene expression, enhancers, TADs, subTADs, and subcompartments of models trained at different resolutions (Fig. 5d), shows that for small scale phenomena and expression like gene expression and enhancers, the cumulative prediction score worsens with coarser resolution as expected. For enhancers, the prediction score drops by 0.22 units when the resolution goes from 2 to 500 kbp (Fig. 5d). Both with TADs and subTADs, the model at 100 kbp has the best prediction score, closely followed by the model at 10 kbp (Fig. 5d). We attribute this performance to the fact that these resolutions, combined with our frame length of 150, are close to the to the averages sizes of both these elements. The model at 500 kbp performs best at identifying subcompartments given that the average size of subcompartments is 300 kbp (Fig. 5d). These results point to the idea that aggregating representations learnt at different Hi-C resolutions will likely increase prediction performance across elements of all sizes. Such aggregation will also potentially help in alleviating computational bottlenecks, as a model at a particular resolution need not take the broader context into account (see the section “Discussion”).

Feature attribution reveals association with genomic elements driving 3D conformation

Given that our representations capture elements driving 3D conformation, we should be able to identify those elements using our representations. To validate the ability of our representations to locate genomic regions that drive chromatin conformation, we identified which genomic positions have the largest impact on Hi-C contacts, using the technique of feature attribution. Feature attribution is a technique that allows us to attribute the prediction of neural networks to their input features. In this case, it identifies which genomic positions influence which Hi-C contacts. We ran feature attribution analysis on the Hi-C-LSTM and aggregated the feature importance scores across all the dimensions of the input representation to get a single score for each genomic position (see the “Methods” section for more details). We expected to see higher feature attribution for the genomic elements, regions, domains, and transcription factors (TFs) that are crucial for chromatin conformation.

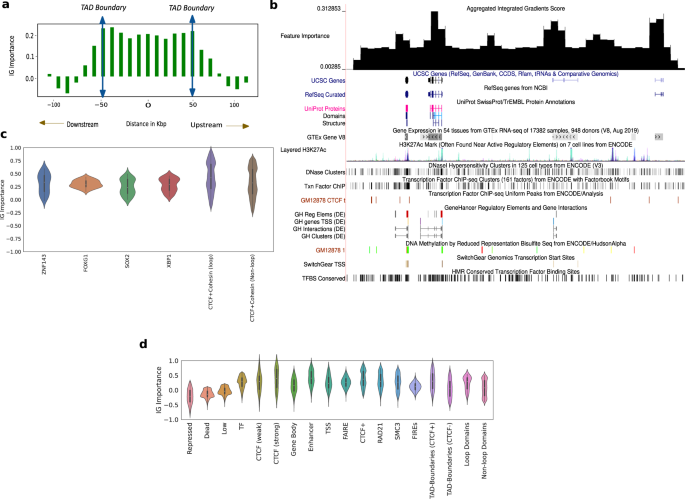
The variation of the aggregated feature importance across interesting genomic regions helps us distinguish boundaries of domains and genomic regulatory elements (Fig. 6a, b). We observe the variation of the feature importance signal across TADs and a selected portion of chromosome 21 (28–29.2 Mbp)⁵⁴ to check if we can isolate the boundaries of domains, genes and other regulatory elements. To deal with TADs of varying sizes, we partition the interior of all TADs into 10 equi-spaced bins and average the feature importance signal within these bins. We plot this signal along with the signal outside the TAD boundary 50 kbp upstream and downstream, averaged across all TADs (Fig. 6a). The feature importance has largely similar values in the interior of the TAD, noticeably peaks at the TAD boundaries, and slopes downward in the immediate exterior vicinity of the TAD (Fig. 6a). This trend validates the importance of TADs and TAD boundaries in chromatin conformation. We also consider a candidate region in chromosome 21 that is referred to in ref. ⁵⁴ to observe the variation of feature importance across active genomic elements (Fig. 6b). For this selected region in chromosome 21, as we do not have to deal with domains of varying sizes, we just average the feature importance signal within a specified number of bins and plot this in the UCSC Genome Browser along with genes, regulatory elements, GC percentage, CTCF signal, and conserved TFBS among others. The feature importance peaks around genes, regulatory elements and domain boundaries (Fig. 6b), showing that they play a more important role in conformation than other functional elements. The feature importance peaks also correlate with CTCF peaks and GC percentage peaks (Fig. 6b).

a The IG feature importance averaged across different TADs of varying sizes. The vertical axis indicates the average IG importance at each position and the horizontal axis refers to relative distance between positions in kbp, upstream/downstream of the TADs. b The IG feature importance for a selected genomic locus (chr21 28–29.2 Mbp) along with genes, regulatory elements, GC percentage, CTCF signal, and conserved TFBS among others in the UCSC genome browser. We see that the feature importance scores peak at known regulatory elements, higher GC percentage, and CTCF peaks. c Violin plots of aggregated feature attribution scores for top ranked transcription factor binding sites (TFBS). The x-axis shows the labels/elements and the y-axis displays the z normalized feature importance scores from Integrated Gradients. Both at loop and non-loop regions, the scores shown are aggregated only at shared sites. d Violin plots of aggregated feature attribution scores for selected elements. The x-axis shows the labels/elements and the y-axis displays the z normalized feature importance scores from Integrated Gradients. The scores for CTCF and Cohesin subunits are aggregated genome wide. In c, d, Violin plots present summary statistics where the white dot is the median, thick gray bar is the inter-quartile range, and thin gray line is the rest of the distribution. Kernel density estimation is shown on either side of the line. Sample size for the genomic elements are calculated genome wide by considering all observations of elements according to element specific data.

We analyzed importance scores at TF binding sites (TFBS)⁵⁵ and saw that some TFBS have a larger positive importance score compared to others (Fig. 6c). Our motif enrichment analysis showed that the top 5 TFs according to importance score were: CTCF, ZNF143, FOXG1, SOX2, and XBP1 (Fig. 6c). As Cohesin is a known partner of CTCF, we looked for Cohesin-binding sites in the ranked list and found them in the top 15. The full ranked list of transcription factors is attached as a Supplementary file. All TFs in the top 5 are known to play a role in chromatin conformation. The genome folds to form “loop domains”, which are found to be a result of tethering between two loci bound by CTCF and Cohesin subunits RAD21 and SMC3⁴⁰. Among the many models of genome folding, Cohesin ring-associated complex that extrudes chromatin fibers and is delimited by CTCF is most promising. This extrusion model explains why loops do not overlap³⁹.

We found that CTCF + Cohesin sites at loop anchors show 10% higher mean importance score than CTCF + Cohesin sites at non-loop regions (we only considered the case where CTCF and Cohesin share sites) and in both cases they have a spread that is predominantly positive (Fig. 6c). Note that CTCF and Cohesin sites usually overlap, so we analyze them together. Specifically, 98% of loop anchor CTCF ChIP-seq peaks also harbor Cohesin peaks; 92% non-loop CTCF peaks do so^56,57. The high feature importance scores observed at CTCF and Cohesin-binding sites reaffirms the crucial role they play in loop formation^39,40. The importance of CTCF is further validated by the aggregated feature importance (Fig. 6d), showing a markedly positive score near CTCF-binding sites given by Segway⁵⁸, particularly the strong ones (mean importance score of 0.45).

Apart from CTCF, the other TFs in the top 5 are also known to play a role in conformation (Fig. 6c). There is a widespread role of C2H2-ZF proteins in chromatin structure and organization⁵⁹. These TFs are known to promote local chromatin loosening, local chromatin condensation⁶⁰, and control chromatin accessibility through the recruitment of chromatin-modifying enzymes⁵⁹. ZNF143 (2nd-most important) is a C2H2-ZF protein. It is known to bind directly to promoters, connect promoters to distal regulatory enhancers⁶¹, and plays a partner role in establishing conserved chromatin loops⁶¹. Similarly, many FOXG1 (3rd-most important) and related TFs are considered pioneer factors which open closed chromatin and facilitate the binding of other TFs^62,63. The last two TFs in our top 5, SOX2 and XBP1, are also known to play a role in conformation. SOX2 loss is seen to decrease chromatin interactivity genome-wide⁶⁴, and the genomic distribution of XBP1 peaks shows that it binds promoters and potential enhancers^65,66.

Along with the aforementioned TFs, we saw that the model places high importance on regulatory elements, particularly enhancers (mean importance score of 0.4) (Fig. 6d). The active domain types had a higher mean score and a spread that largely occupies the positive portion of the feature importance plot when compared to the inactive regions (Fig. 6d). This is further verified by segway-gbr⁶⁷ feature importance scores (Supplementary Fig. 7). This suggests that active regions may play a dominant role in nuclear organization, where the movement of repressed regions to the periphery is a side-effect.

Aggregated feature importance also demonstrates the largely positive feature attribution of genomic regions that are an integral part of 3D conformation like FIREs, topologically associating domain (TAD) boundaries with and without CTCF sites, loop and non-loop domains (Fig. 6d). TAD boundaries enriched with CTCF show a 20% higher mean importance score compared to TAD boundaries not associated with CTCF, pointing to the importance of CTCF sites at domain boundaries in conformation (Fig. 6d). Moreover, loop domains show a 20% higher mean importance score compared to non-loop domains, which is expected because of the increased contact strength on average and the presence of CTCF sites (Fig. 6d). P-values from the relevant comparisons for each group can be referred to in the Supplementary: Table 1.

Hi-C-LSTM accurately predicts effects of a 2.1 Mbp duplication at the SOX9 locus

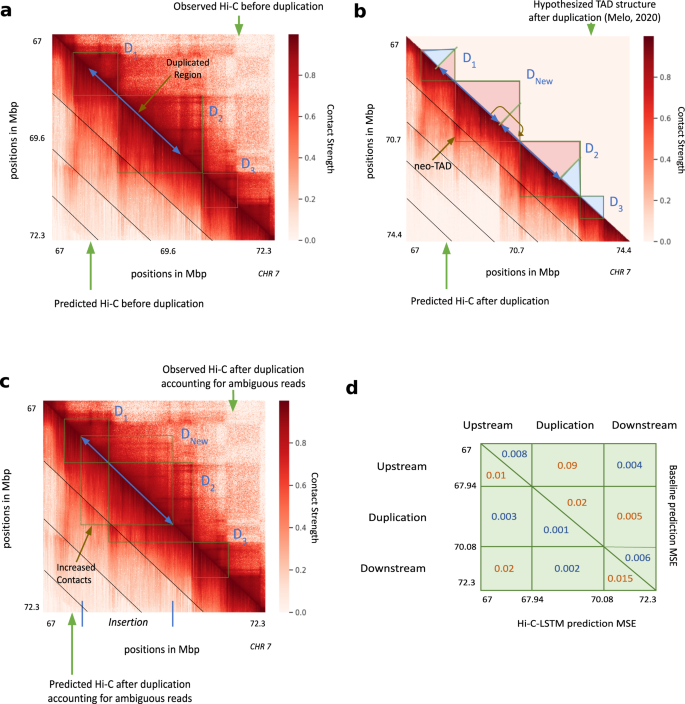
To validate Hi-C-LSTM as a tool for in-silico genome alterations, we simulated a structural variant at the SOX9 locus that was previously assayed by Melo et al. ⁶⁸. This variant was observed in an individual with Cook’s syndrome and comprises the tandem duplication of a 2.1 Mbp region on chromosome 17 that includes regulatory elements of SOX9 (chr17:67,958,880–70,085,143; GRCh37/hg19, Fig. 7a). To simulate a Hi-C experiment on a genome with this variant, we made a new Hi-C-LSTM representation matrix that includes a tandem copy of the representation at the locus in question and passed this representation matrix through the original Hi-C-LSTM decoder to produce a simulated Hi-C matrix on a post-duplication genome (Fig. 7b). Because Hi-C reads cannot be disambiguated between the two duplicated loci, we simulated mapping reads to the observed hg19 reference by summing reads originating from the two copies (see the “Methods” section). We evaluated Hi-C-LSTM’s predictions according to the agreement between this predicted matrix and a Hi-C experiment performed by Melo et al. ⁶⁸ (Fig. 7c).

In all subplots, upper and lower triangles denote observed and predicted Hi-C contact probabilities respectively, and diagonal black lines denote Hi-C-LSTM frame boundaries. a Observed and predicted Hi-C before duplication. D₁, D₂ and D₃ indicate the three pre-duplication topological domains. b Predicted Hi-C after duplication on a simulated reference genome that includes both copies. Lower triangle indicates Hi-C-LSTM predicted contacts. The true Hi-C contact matrix on this reference genome is not observable because the read mapper cannot disambiguate between the two copies. The upper triangle depicts the post-duplication topological domain structure hypothesized by Melo et al, which includes a novel topological domain D_New. c Observed and predicted Hi-C on the observed pre-duplication reference genome. Upper triangle shows observed post-duplication Hi-C data assayed by Melo et al. Lower triangle shows Hi-C-LSTM predictions, mapped to the pre-duplication reference by summing the contacts for the two copies (see the section “Results”). d Average mean-squared error (MSE) in predicting the observed data by (lower triangle) Hi-C-LSTM, and (upper triangle) a simple baseline (see the section “Results”) at the upstream, duplicated, and downstream regions.

We found that Hi-C-LSTM accurately predicted the effect of the duplication. The domains that existed pre-duplication (D₁, D₂, D₃, Fig. 7a) are correctly captured post-duplication. In addition, a new chromatin domain (D_New) that was introduced by the duplication is correctly predicted by Hi-C-LSTM (Fig. 7b). To quantitatively evaluate our predictions, we compared them to a baseline that predicts the observed pre-duplication Hi-C for the interactions between the upstream, downstream and duplicated regions, and the genomic average for the interactions of the duplicated region with itself (see the “Methods section). We found that Hi-C-LSTM’s predictions significantly outperform this baseline overall (Fig. 7d). Note the baseline is a slightly better predictor of contacts between the upstream and downstream regions.

Hi-C-LSTM’s predictions have the advantage that they describe contacts on the true post-duplication genome, in contrast to the reference genome used to map reads (Fig. 7c). Hi-C-LSTM’s contacts recapitulate the post-duplication topological domain structure hypothesized by Melo et al. These duplication experiments validate the ability of Hi-C-LSTM to perform in-silico insertion and duplication.

Note that Hi-C-LSTM can simulate only cis effects such as structural variants, but not trans effects that arise from loss of diffusible entities such as transcription factors.

Hi-C-LSTM can simulate knockout of transcription factor binding sites and TAD boundaries

As Hi-C-LSTM is able to perform in-silico insertion/duplication (see the section “Duplication”), we wanted to investigate whether knockout or deletion of certain genomic loci would produce reliable changes in the resulting Hi-C contact map. In-silico knockout experiments have gained prominence lately, mainly in intercepting signal flows in signaling pathways⁶⁹ and drug discovery^70,71,72. A Hi-C in-silico manipulation tool is of great value it enables researchers to identify the importance and influence of any genomic locus of interest to 3D chromatin conformation.

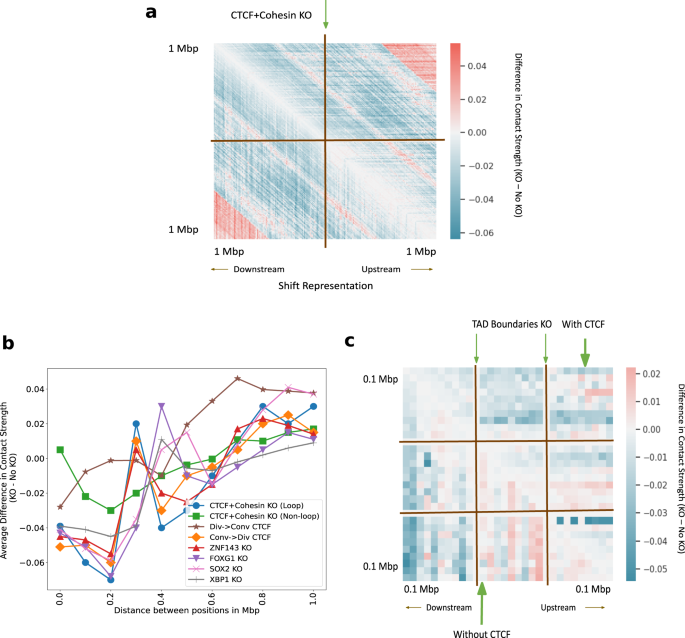
It is an open question how to simulate small-scale perturbations. We performed knockout using four different techniques at CTCF plus Cohesin-binding sites (see the section “Discussion”). The difference in inferred Hi-C between the CTCF plus Cohesin knockout and the no knockout using shifted representations (see the section “Methods”) shows the decrease in contact strength (7% lower on average) in the immediate neighborhood of the KO site (Fig. 8a). Other ways to simulate knockout like using the padding, zero and average representations (Supplementary: Fig. 8) exploit different properties of the model. We believe there is no one right way to perform knockout, however, we prefer the method of shifting all downstream representations from the knockout site upward (see the “Methods” section).

a The average difference in predicted Hi-C contact strength between CTCF + Cohesin knockout (KO) and no knockout in a 2 Mb window. We simulate deletion by shifting the downstream representations upward. b Average difference in contact strength of the inferred Hi-C matrix between knockout and no knockout (y-axis) for varying distance between positions in Mbp (x-axis). The knockout experiments include TFBS knockout and convergent/divergent CTCF replacements (legend). c The genome-wide average difference in predicted Hi-C contact strength between TAD boundaries knockout and no knockout with CTCF (upper-triangle) and without CTCF (lower-triangle).

Previous work showed that altering even a single base pair near the loop anchors can make many loops and domains vanish, altering chromatin conformation at the megabase scale³⁹. Given the crucial role played by CTCF and Cohesin subunits in conformation at loop anchors (see sections “Classification”, “Attribution”), we hypothesized that knocking out CTCF and Cohesin subunit binding sites will alter the Hi-C contact map in the neighborhood. The average difference in predicted contact strength between no knockout and knockout at the site under consideration as a function of genomic distance is observed (Fig. 8b). After the combined CTCF and Cohesin knockouts, the average contact strength reduces by 7% in a 200 kbp window when compared to the no knockout case (Fig. 8b). CTCF knockout is seen to affect insulation and reflect possible loss of loops at 200 kbp (Fig. 8b). The knockout of CTCF and Cohesin subunit binding sites at non-loop regions^56,57 (just like feature attribution, we only considered the case where CTCF and Cohesin share sites, and ignored the cases where CTCF binds alone, and Cohesin binds alone) produces markedly different effects with 2% lower average inferred strength after knockout at 200 kbp, hinting at the relative importance of loop and non-loop binding factors (Fig. 8b).

Along with CTCF, we knocked out the other 4 TF binding sites (TFBS) in the top 5 TFs according to the ranked list, namely, ZNF143, FOXG1, SOX2, and XBP1 (Fig. 8b). We see that the average predicted contacts after genome-wide knockout partially reflects the importance attributed to each TF by integrated gradients. FOXG1 binding site knockout reduces contacts by 7% on average, XBP1 binding site knockout reduces contacts by 4% on average, whereas ZNF143 and SOX2 binding site knockouts reduce contacts between 4% and 5% on average at 200 kbp. Most knockouts cause an increase in contacts at 300Kbp and a gradual increase in contacts after 400 kbp. These results validate that Hi-C-LSTM knockout of TFBS captures the general idea of contacts depleting within the domain and connecting regions outside the domain.

The CTCF sites at loop anchors occur mainly in a convergent orientation, with the forward and reverse motifs together, suggesting that this formation maybe required for loop formation^{18,73,74,75,76,77,78} (see Supplementary Fig. 9 for illustration). To check how important the orientation of CTCF motifs is to conformation, we conducted CTCF orientation replacement experiments at loop boundaries. The average difference in predicted contact strength between no replacement and replacement at the site under consideration as a function of genomic distance is observed (Fig. 8b). The replacement of convergent with the divergent orientation around loops is seen to behave similar to the case of CTCF knockout thereby validating observations made in⁷⁹ (Fig. 8b). On the other hand, replacement of divergent with the convergent orientation is seen to preserve loops at 200 Kbp and behave similar to the control (Fig. 8b).

TADs anchored with CTCF at their boundaries have a differential role to play in conformation compared to the TADs without CTCF. We wanted to check if Hi-C-LSTM can capture this differential behavior of TADs by knocking out their boundaries. To deal with TADs of varying sizes, we partition the interior of all TADs into 10 equi-spaced bins and average the predicted contacts within these bins. We show these along with the regions outside the TAD boundary 100Kbp upstream and downstream, averaged across all TADs (Fig. 8c). The average difference in inferred Hi-C between the knockout at TAD boundaries and the no knockout (Fig. 8c) shows largely decreased contacts for both TADs with and without CTCF in a 200 kbp window (3% lower on average). Within the TAD, however, we see increased contacts for TADs without CTCF (5% higher on average) and decreased contacts with CTCF (4% lower on average) (Fig. 8c).

Simulating loop anchor deletions at the TAL1 and LMO2 loci Hi-C-LSTM predicts measured 5C data

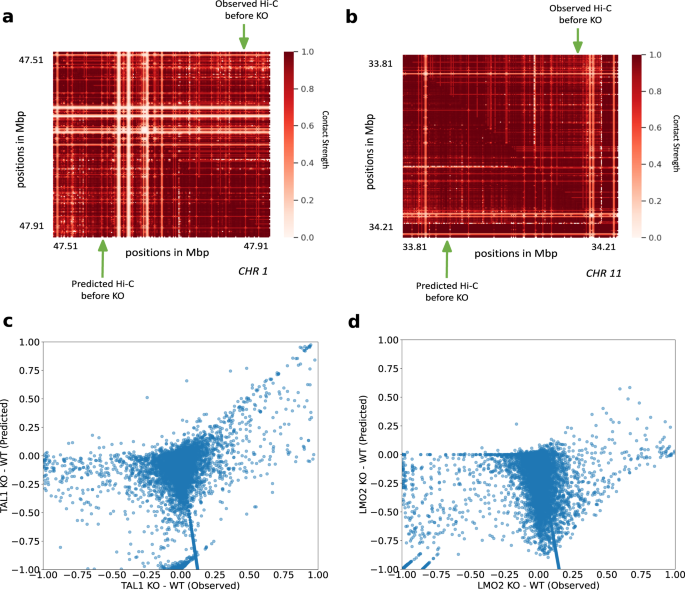
To further validate the ability of Hi-C-LSTM to predict experimental perturbations, we simulated the deletion of loop anchor regions at the TAL1 and LMO2 neighborhood boundaries in human embryonic kidney cells (HEK-293T) previously conducted by Hnisz et al.⁸⁰. These deletions were observed in T-cell acute lymphoblastic leukemia (T-ALL) patients. The TAL1 anchor deletion was seen on chromosome 1 in the neighborhood of 47.7 Mbp (GRCh37/hg19, Fig. 9a), and the LMO2 anchor deletion was seen on chromosome 11 in the neighborhood of 34 Mbp (GRCh37/hg19, Fig. 9b)⁸⁰. Both deletions included loop boundary sites. The authors hypothesized that deletions of loop boundary sites at these loci could cause activation of inactive proto-oncogenes within the loops⁸⁰. To simulate a Hi-C experiment on a genome with these deletions, we first obtained the trained model from GM12878 and retrained it on the 5C data from the TAL1 and LMO2 segments⁸⁰. We then made a new representation matrix that shifted the representations downstream from the knockout sites upward, and passed this representation matrix through the retrained Hi-C-LSTM decoder to produce a simulated Hi-C matrix (Supplementary Fig. 10a, b, lower-triangle) (see the “Methods” section for more details) and compared this with the 5C experiment performed by Hnisz et al. ⁸⁰ (Supplementary Fig. 10a, b, upper-triangle).

a, c TAL1 anchor deletion on chromosome 1. a Observed Hi-C contacts before deletion (upper-triangle), and predicted Hi-C contacts before deletion (lower-triangle). c Scatter plot of differences in contacts after and before TAL1 deletion. The x-axis shows observed differences, and the y-axis shows predicted differences. b, d LMO2 anchor deletion on chromosome 11. b Observed Hi-C contacts before deletion (upper-triangle), and predicted Hi-C contacts before deletion (lower-triangle). d Scatter plot of differences in contacts after and before LMO2 deletion. The x-axis shows observed differences, and the y-axis shows predicted differences, KO knockout, WT wild-type.

They authors saw that the insulated neighborhoods of TAL1 and LMO2 were disrupted, which allowed activation of these elements by regulatory elements outside the loop, and caused rearrangement of interactions around the neighborhood. We found that Hi-C-LSTM’s predicted contacts correlate with the post-deletion interactions hypothesized by Hnisz et al. To evaluate our predictions, we investigated whether there is a correlation in the differences of knockout and no knockout between the observed and the predicted contacts (Fig. 9c, d). We found a noticeable correlation between Hi-C-LSTM’s prediction differences between knockout and no knockout and the observed assayed contacts for TAL1 (Fig. 9c). The interactions across domain boundaries that did not exist pre-deletion in the TAL1 neighborhoods were correctly captured by Hi-C-LSTM (Fig. 9c). The correlation for LMO2 was not as strong as TAL1 (Fig. 9d) and the discrepancy was particularly at points where the post knockout contacts were same as the pre-knockout or higher. We see that Hi-C-LSTM accurately predicts decrease in post knockout contacts as decrease, but wrongly attributes some points of no-change and increase as decrease (Fig. 9d).

These anchor deletion experiments reaffirm that Hi-C-LSTM can perform in-silico alterations with moderate accuracy. Moreover, the results also point to the transfer learning ability of Hi-C-LSTM in cell types with limited data (see the section “Discussion”).

Frequently interacting region (FIRE) scores were converted to binary indicators using 0.5 as a threshold following⁹⁵. See the section “Data availability” for links to FIRE data.

An LSTM’s output is determined by the following series of operations⁴¹.

A trained Hi-C-LSTM model consists of LSTM parameters (see section “LSTM”) and a representation matrix \(R\in {{\mathbb{R}}}^{N\times M}\), where M is the representation size. At each genomic position, (i, j) pair is given as input to an embedding layer, which indexes the row and column representations \({{{{{{{{\boldsymbol{R}}}}}}}}}_{{{{{{{{\boldsymbol{i}}}}}}}}},{{{{{{{{\boldsymbol{R}}}}}}}}}_{{{{{{{{\boldsymbol{j}}}}}}}}}\in {{\mathbb{R}}}^{M}\) and feeds these two vectors as input to the LSTM. The output of the LSTM is the predicted Hi-C contact probability \({\hat{H}}_{i,j}\) for the given (i, j) pair.

The hidden states of the LSTM are carried over from preceding columns thereby maintaining a memory for the row. For the sake of memory usage, the hidden states are reinitialized after every each frame of 1.5 Mbp or 150 resolution bins (see section “Modeling Choices”). This process is repeated for each row of the Hi-C matrix (Eq. (3)).

We employed PyTorch, a Python-based deep learning framework and trained Hi-C-LSTM on GeForce GTX 1080 Ti GPUs with ADAM as the optimizer¹⁰⁵. All parameters in PyTorch were set to their default values while training. As our primary goal was not to infer values for unseen positions but to form reliable representations for every chromosome, we trained our model on the full genome. For our Hi-C reproduction evaluation, we trained the representations on the full genome but the decoders only on a random subset. We chose to train the decoders on a random subset of the genome to prevent the decoder from overpowering the representations. The time taken to train and test all methods is included in the Supplementary Table 3 (Running Time).

To choose the representation size of our model, we performed an ablation analysis. We computed the average mAP across all downstream tasks with the Hi-C-LSTM model which consists of a single layer, unidirectional LSTM with layer norm in the absence of dropout¹⁰⁶ for odd chromosomes and used the even chromosomes to validate whether the choice of hyperparameters remained the same irrespective of chromosome set. We observed the mAP (see “Methods” section) of the Hi-C-LSTM vs. increasing representation size along with Hi-C-LSTM that is bidirectional, in the presence of dropout, without layer norm and 2 layers (Supplementary Fig. 13). While both the presence of dropout and the absence of layer norm adversely affected mAP, the addition of a layer and a complimentary direction did not yield significant improvements in downstream performance. We conducted a similar ablation experiment and computed the average Hi-C R-squared for the predictions with increasing representation size (Supplementary Fig. 13) and observed that the performance trend is preserved, which was indicative of the fact that recreating the Hi-C matrix faithfully aids in doing well across downstream tasks. These results were verified to be true for even chromosomes as well (Supplementary Fig. 13). For both odd and even chromosomes, even though the Hi-C prediction accuracy increased with hidden size, we noticed the elbow at a representation size of 16 for average mAP and therefore set our representation size to that value as a trade-off.

We investigated three hypotheses with following analysis. First, we asked whether the Hi-C-LSTM representations faithfully construct the Hi-C matrix. Second, whether the Hi-C-LSTM representation and the decoder are both powerful in generating the Hi-C map. Third, we evaluated the utility of the representations to infer a replicate map. In all cases, we computed the average prediction accuracy in reconstructing the Hi-C contact matrix, measured using R-squared, which represents the proportion of the variance of the observed Hi-C value that’s explained by the Hi-C value predicted by the Hi-C-LSTM. We sampled the means of observed Hi-C values at different distances between positions and used that as a baseline.

In our second experiment (Fig. 3b), we trained the representations on replicate 1 using all chromosomes, and repeated the aforementioned decoder training process on replicate 2.

We conducted both these experiments in all 4 cell types, namely, GM12878 (Fig. 3a, b), H1-hESC (Fig. 3c, d), HFF-hTERT (Supplementary Fig.1a, b), and WTC11 (Supplementary Fig.1c, d).

For each type of element, we first trained a boosted decision tree classifier called XGBoost⁵³ on the representations. We tried tree boosting first as it is shown to outperform other classification models with respect to accuracy when ample data is available. Following Avocado⁹⁵, we used XGBoost with a maximum depth of 6 and a maximum of 5000 estimators and these parameters were chosen following ablation experiments with odd chromosomes as the training set and even chromosomes as the test set (Supplementary Fig. 15). N-fold cross-validation, with n = 5, was used to validate our training with and an early stopping criterion of 20 epochs. The rest of the XGBoost parameters were set to their default values.

For each task, the genomic loci under contention were assigned labels. All tasks were treated as binary classification tasks, except the subcompartments task, which was treated as a multi-class classification task. For tasks without preassigned negative labels, negative labels were created by randomly sampling genome-wide, excluding the regions with positive labels. We sampled negative labels until the number of negative labels equaled the number of positive labels to avoid class imbalance during classification. The XGBoost classifier was given the representations at these genomic loci as input and the assigned labels as targets.

We then compared the XGBoost classifier trained separately for each task with a multi-class multi-label classifier with a simple linear layer and sigmoid output. We observed that the multi-class classifier, which predicted regions/domains the given position belonged to, was much faster and gave more reliable results when compared to the XGBoost classifier. Therefore, we prefer the linear classifier for classification.

The classifiers were evaluated using four standard metrics for classification tasks, namely, mean average precision (mAP) (otherwise known as area under the Precision-Recall curve (AuPR)), area under the Receiver Operating Characteristic curve (AuROC), Accuracy (\(A=\frac{{\rm {TP+TN}}}{\rm {{TP+FP+TN+FN}}}\)), and F-score. AuROC is defined as the area under the curve that has true positive rate (\({\rm {TPR}}=\frac{{\rm {TP}}}{{\rm {TP+FN}}}\)) on the y-axis and false positive rate (\({\rm {FPR}}=\frac{\rm {{FP}}}{\rm {{FP+TN}}}\)) on the x-axis. mAP is defined as the average of the maximum precision (\(P=\frac{{\rm {TP}}}{\rm {{TP+FP}}}\)) scores achieved at varying recall levels (R = TPR). F-score is defined based on precision and recall (\(F=\frac{2P* R}{P+R}\)). We compared these metrics for GM12878, H1-hESC, and HFF-hTERT (see Supplementary Figs. 4–6 for more details).

The Hi-C-LSTM enables us to perform in-silico deletion, orientation replacement and reversal of genomic loci and predict changes in the resulting Hi-C contact map. We performed three types of experiments:: knockout, CTCF orientation replacement, and duplication. In a knockout experiment, we chose certain genomic sites (such as CTCF and Cohesin binding sites) and replaced their representations with a different representation depending on the method used to perform the knockout (Supplementary Fig. 8).

Among the four possible methods to perform knockout, we prefer the method of shifting the representations. Shifting the representations not only captures the true post-duplication genome but also avoids the noise that comes from zeroing or averaging the representations in the neighborhood (Supplementary Figs. 8, 16). It also is more interpretable than using the padding representation (Supplementary Figs. 8, 16) because we do not fully understand the role of padding representations in recreating the Hi-C matrix. The knockout of the representation at a particular row affects not just the Hi-C inference at columns corresponding to that row but also the succeeding rows because of Hi-C-LSTM’s sequential behavior. The LSTM weights remain unchanged, but as the input to the LSTM is modified, the inferred Hi-C contact probability is altered based on the information retained by the LSTM about the relationship between the sequence elements under contention and chromatin structure.

In a CTCF orientation replacement experiment, we replaced the representations of downstream-facing CTCF motifs with the genome-wide average of the upstream-facing motifs and vice versa. This was done under the assumption that the average representation of the given orientation would encapsulate the important information regarding the role played by the orientation in chromatin conformation.

Our anchor deletion experiment was carried out by first obtaining the trained Hi-C-LSTM model from GM12878, and retraining it on the 5C data from the TAL1 and LMO2 segments in HEK-293T⁸⁰. The TAL1 fragment is on chromosome 1 from 47.5 to 47.9 Mbp, and the LMO2 fragment is on chromosome 11 from 33.8 to 34.2 Mbp (GRCh37/hg19). After retraining the model with data from HEK-293T, we made a new representation matrix by shifting all the downstream representations upward (Supplementary Fig. 8), and passed this representation matrix through the retrained Hi-C-LSTM decoder to produce the inferred Hi-C matrix (Supplementary Fig. 10).